rangifer’s diary: pt. xci
What’s our level range, again?
If you’ve ever done “points farming” or BRPQ (“Boss Rush Party Quest”; BPQ) during a MapleLegends event, then you already know how party recruitment goes. For farming event points, you’re looking for fellow HHGII-goers (or PP1-goers, or what have you) that are within 20 levels of you.
In this context, “ is within levels of ” means that the absolute difference between the levels of PCs and is less than or equal to . Symbolically, we’d write this as , where is ’s level. For event-point farming, ; for BRPQ, .
Tolerance
You’ll notice that “ is within levels of ” sounds exactly like some kind of binary relation. More specifically, for a given value of , this is a homogeneous relation over , where is the set of all PCs (). This homogeneous relation — which we’ll just call — has some nice properties:
- is symmetric, because the absolute difference commutes.
- is reflexive for any , because the level difference between a PC & themself is always 0. We don’t care about the case, because it’s trivial — it’s just the empty relation.
However, it also lacks some properties that we’re familiar with having in many binary relations:
- is not transitive. This is really important for various reasons (one reason being that this makes not an equivalence relation), & is obvious if you just think about it for a second: if is level 30, is level 45, & is level 60, then and , but not (because ).
- is not connected. In particular, if the absolute difference between the levels of and is in excess of , then and are “incomparable” according to this relation (viz. neither nor hold).
Like I said, can’t be an equivalence relation because it lacks transitivity. However, I found out that there’s actually a special name for this kind of relation: a tolerance relation. The name makes sense: we essentially have some level of “tolerance” (which in our particular case is called ) for how “distant” objects may be from one another before we consider them to be “discernible” from one another. Equivalence relations (or rather, congruence relations) are the special case of tolerance relations where the “tolerance” is “zero”, or is otherwise nonexistent in some sense; then, it’s not possible for “tolerances” to “accumulate” (as they do in the “” example above) & cause intransitivity. In the language of tolerance relations, when holds, we say that “ is indiscernible from ”. This makes a tolerance space.
Furthermore, a tolerance relation over a finite set is called a dependency relation. Dependency relations are important in concurrent computation, where they are so called because they relate two objects iff those objects depend on one another in some way, thus precluding them from being computed concurrently. For example, if you want to cook some food & then eat it, then there is a dependency between the “cooking” part & the “eating” part; you cannot do them concurrently — unless you actually wanted to eat the uncooked food, in which case, why even bother cooking in the first place?
Aggregate tolerance
In our particular case of recruiting for a party (whether it be for farming event points, or for BRPQing, or for something similar), we ideally want — and, in the case of BRPQ, absolutely need — this tolerance relation to hold pairwise for all members of the party. Symbolically, if our party is (s.t. ), then we want:
With this in mind, there’s a particular phenomenon that we quickly notice: as the party’s size (i.e. its number of members) grows, we see a shrinking of the range of levels that a new member could possibly be. For example, if we represent our party as a multiset of levels, & we let , then we might start with e.g. , & the range of levels that a new member could possibly be is . If we select some arbitrary level from this interval, let’s say e.g. 110, then our party is , & the valid level interval for a new member is now , which is a strict subset of the original interval. In general, adding a new party member does not necessarily change the valid level interval, so the new interval is always a subinterval (not necessarily strict) of the old one. This means that the length of the interval decreases weakly monotonically as the party size grows.
In particular, the valid level interval for a new party member, as a function of the multiset of levels of the current party members (call this multiset ), is:
(Note that an interval like — where the lower bound is strictly greater than the upper bound — is the empty set.)
As a result, the interval only changes if the new member (we’re not going to consider the possibility of members leaving the party or being kicked out) changes the maximum level or minimum level present in the party. In other words, the interval only changes if the new member’s level is either strictly greater than, or strictly less than, all old member’s levels.
Interval/bound convergence
I noted that the length of the interval decreases weakly monotonically as the party size grows; in fact, it’s clear that it can “converge” to an absolutely minimal length of . This occurs when , & thus . At exactly this point, it no longer matters how many new members join, nor what levels those new members are — the interval will never change.
We don’t typically have any way to accurately predict the level of the next PC who will ask to join the party — we’re usually just recruiting whichever random people happen to show up at that time. Thus, we’ve no good choice but to model the level of a new party member as effectively a random variable. In doing so, assuming that we assign a nonzero probability to each level[1], we can intuitively[2] see that almost surely converges to , as the party size tends to +∞.
Given that we expect to converge in this way after a sufficient number of new members join our party, the question that I want to ask seems simple: how long does it take to converge?
To answer this question, we need to define things in a way that is a bit more clear-cut. When we say “how long”, we really mean “how many new party members”; each time that a new party member is added, I call this a single step of the process.
Furthermore, as it is, there’s actually no guarantee that we converge at all, because we’re still talking about MapleStory parties, which are limited to a maximum cardinality of 6. So we want to lift that restriction, allowing arbitrarily large (but still always finite) parties.
Similarly, we want to lift the level restrictions that MapleStory inherently possesses, because it makes things more asymmetrical & more difficult to reason about. If and , then the formula above suggests that ; but in practice, it’s actually , because the maximum level in MapleStory is 200. So instead, we’ll assume that any element of ℤ is a valid level for a PC to have, & anything else (e.g. 13.5, π, ♣, &c.…) is invalid. Also similarly, we want to constrain so that .[3]
Another part that we have to specify is how PC levels are distributed. We’ve already accepted that the level of a new party member is random, but we’ve yet to specify in what way. By invoking the principle of indifference, we can just assume that PC levels are distributed uniformly. Obviously, in practice, the “actual” (empirical) distribution is not strictly uniform; for example, level 120 characters are probably more common than level 119 characters in MapleLegends. But trying to get a better approximation is almost certainly more trouble than it’s worth, & much more importantly, we don’t actually care; although this problem is modelled on empirical player-driven phenomena that occur in (a particular implementation of) MapleStory, it’s really just a mathematical problem that we have in mind.
WLOG (we’ll get a better idea of why this doesn’t lose generality in just a bit), we can assume for simplicity that our initial value of is . Then, given some value of , we want to ask: what is the probability that we converge after steps ()? What we’re asking for here is a probability mass function (PMF) that is parameterised by . Because this PMF more or less defines[4] the probability distribution that we’re after, I’m going to refer to the PMF as simply , where RBC stands for “recruitment bound convergence”. Then, is the probability that, given some value for , we converge in exactly steps.
Why do we care about ? Iunno. I just thought of it one time when I was farming event points or something. Sue me. The point is that I spent absolutely way too long obsessing over it, & it is now that we will see what I’ve uncovered about this mysterious probability distribution. I’m going to go over what I learned in roughly the order that I learned it, & with roughly the methods by which I learned it.
Footnotes for “Interval/bound convergence”
- [↑] At least, to every level that is valid for a PC to be, which in MapleStory is usually . Of course, merely assigning a nonzero probability to each level in does the trick, as well.
- [↑] By waving our hooves & invoking the infinite monkey theorem, or something…
- [↑] In general, we could loosen the constraints on so that it merely has to be a nonnegative real number. However, if we do this, then and are effectively the same, so it’ll make things a lot easier to just assume by convention that is a natural number.
- [↑] See also: Probability space.
Phase I: Worked examples
Because this whole thing was a little too abstract, I decided to first make it concrete by working out, by hoof, a particular example.
Consider . What’s the probability that we converge in exactly 1 step? In other words, what’s the value of ? Well, we converge in exactly 1 step iff the first PC to join the party is level 4 or is level −4. We can see that , so the set of possible levels that this first step could add to the party is the intersection of this interval with , viz. . The cardinality of this set is 9, & there are 2 possible values in the set that cause us to converge (viz. −4 and 4), so . Easy, right?
Okay, but what about ? Well, we can take advantage of the symmetry of to observe that, in the first step, adding a level PC to the party is the same as adding a level PC to the party. More generally, instead of laboriously tracking the exact state of at each step, we can note that we really only care about , which itself only depends on and . So, because levels are distributed uniformly (meaning that is effectively invariant under constant shifts[1], e.g. adding +17 to all levels), we can simply pretend that . For example, we’d simplify to , & we’d simplify to as well. These observations & simplifications will make it significantly easier to compute values of by hoof, but will also contribute to a more systematic (read: not by hoof) treatment of . Working through the calculation of , we end up with something like:
| we add | valid new levels | we add | probability | |
|---|---|---|---|---|
| −3, 3 | −1, 0, 1, 2, 3, 4 | −1, 4 | ||
| −2, 2 | −2, −1, 0, 1, 2, 3, 4 | −2, 4 | ||
| −1, 1 | −3, −2, −1, 0, 1, 2, 3, 4 | −3, 4 | ||
| 0 | −4, −3, −2, −1, 0, 1, 2, 3, 4 | −4, 4 |
These four cases make up all possible cases where we converge in exactly two steps: with our simplifications, there are only four possible levels that we can effectively add in the first step without converging (we can’t converge at that point because then it would be converging in exactly one step instead of two); & then we always have to choose a level that causes us to converge in the second step, of course.
Notice that no matter how many steps we converge in, there are always exactly two possible levels that can be added to in the final step to make it converge: either the level that’s exactly high enough to converge, or that’s exactly low enough. Because these four cases are exhaustive, we can simply add their probabilities to get the value of
That was a slight bit of a pain in the ass, but don’t worry — it gets way more painful from here. What about ? Prepare to be sorry that you asked:
| we add | valid new levels | we add | valid new levels | we add | probability | ||
|---|---|---|---|---|---|---|---|
| 0 | −4, −3, −2, −1, 0, 1, 2, 3, 4 | 0 | −4, −3, −2, −1, 0, 1, 2, 3, 4 | −4, 4 | |||
| −1 1 | −3, −2, −1, 0, 1, 2, 3, 4 | −3, 4 | |||||
| −2 2 | −2, −1, 0, 1, 2, 3, 4 | −2, 4 | |||||
| −3 3 | −1, 0, 1, 2, 3, 4 | −1, 4 | |||||
| −1, 1 | −3, −2, −1, 0, 1, 2, 3, 4 | 0 1 | −3, −2, −1, 0, 1, 2, 3, 4 | −3, 4 | |||
| −1 2 | −2, −1, 0, 1, 2, 3, 4 | −2, 4 | |||||
| −2 3 | −1, 0, 1, 2, 3, 4 | −1, 4 | |||||
| −2, 2 | −2, −1, 0, 1, 2, 3, 4 | 0 1 2 | −2, −1, 0, 1, 2, 3, 4 | −2, 4 | |||
| −1 3 | −1, 0, 1, 2, 3, 4 | −1, 4 | |||||
| −3, 3 | −1, 0, 1, 2, 3, 4 | 0 1 2 3 | −1, 0, 1, 2, 3, 4 | −1, 4 |
Fun!!! Adding up the probabilities of these (exhaustive) cases gets us:
I think that’s about enough of that…
Footnotes for “Phase I: Worked examples”
- [↑] More formally, the elements of are points in an affine space. This affinity is naturally induced by the fact that is defined in terms of subtraction between these “points”.
Phase II: What’s the probability that we converge in exactly steps?
Now that we’ve worked a good way through an example, we’re gonna try to make the leap to a generalisation. I did a lot of scribbling nonsense, & a lot of thinking really hard about it, & I’m gonna try to give a brief explanation of my reasoning.
First of all, we’re going to define a new variable called , which represents the difference (you can also think of it as standing for “distance” or “diameter”) between & . In other words, the simplification of that I defined above can be defined as simply .
As I was trying to come up with a general solution, I started scribbling out some pseudocode, & ended up with something like this to capture the general structure of the example used in Phase I — in particular, :
sum a ← [-3..3]:
d_a := |a|
sum b ← [(d_a - 3)..3]:
d_b := max{d_a - b, b, d_a}
sum _ ← [0, 1]:
1/9 * 1/(9 - d_a) * 1/(9 - d_b)
I’m using the sum a ← [-3..3]: notation to mean that we’re summing over a, with the values of a being taken from the list [-3..3] (which, in Haskell notation, is the same as the list [-3, -2, -1, 0, 1, 2, 3]), & the summands simply being the value(s) that the block takes on (which may themselves be summations…). I’m also using := for assignment.
As you can see, I’m essentially just summing over all possible cases, i.e. every possible level that the first added party member could have, combined with every possible level that the second added party member could have, & so on. In the first two sum loops, we’re avoiding convergence & considering every remaining possibility, and in the third & final sum loop, we just consider the two cases that cause convergence — which is why there’s no summation variable, & instead just a blank _ — I’ve used the list [0, 1], but any list of length two would work equally well.
The pattern here is hopefully clear: if we wanted to consider larger values of like , then we would just add another sum layer (sum c ← [(d_b - 3)..3]:, ⋯) that calculates yet another value of (d_c := max{d_b - c, c, d_b}, ⋯), & the arithmetic expression in the innermost sum loop would look like 1/9 * 1/(9 - d_a) * 1/(9 - d_b) * 1/(9 - d_c) * ⋯.
Of course, there’s also the question of how I came up with “max{d_a - b, b, d_a}” in the first place. I basically came up with this expression by considering two cases, which are together exhaustive: that the summation variable is negative, & that is nonnegative:
- If is negative, then is increased by (or in other words, decreased by ). This is because was previously , so the new minimum element of is lower than it previously was, & thus is increased by .
- If is nonnegative, then is increased iff . was previously , so:
- If is somewhere within the interval , then does not change (i.e. ).
- If exceeds the interval , then is increased by the amount that exceeds said interval, namely by .
- There are no other cases, as we already assumed to be nonnegative.
In other words:
- If is negative, then .
- If is nonnegative, then .
’ing the “” with 0 covers the “ is somewhere within the interval ” case above, causing to be increased by 0 (i.e. to not change) in that case. Thus, we can refine how we split up the computation of “” above:
- If , then . Thus becomes , which simplifies to just .
- If , then . Thus becomes simply .
So, we now have these three exhaustive cases:
- If is negative, then .
- If is nonnegative, then:
- If , then .
- If , then .
…Which is where “” (max{d_a - b, b, d_a}) comes from.
This brings us to the first implementation of that I came up with that, you know, at the very least didn’t require doing anything “by hoof”. It’s an implementation in Python, with a function called pmf0:
from fractions import Fraction as Q
def pmf0(k, n):
if k == 0:
return Q(1) if n == 0 else Q(0)
elif n < 1:
return Q(0)
return sum(pmf_inner0(k, n, 0))
def pmf_inner0(k, n, d):
denom = 2 * k + 1 - d
if n == 1:
yield Q(2, denom)
else:
for elem in range(d - (k - 1), k):
d_prime = max(d - elem, elem, d)
for f in pmf_inner0(k, n - 1, d_prime):
yield Q(1, denom) * f
pmf0 is entirely correct, and it calculates its result with unlimited precision (using Python’s built-in rational number arithmetic). It is, however, basically the worst implementation — I continued refining it gradually to make something better.
As you’d expect, pmf0 (or rather, pmf_inner0) is recursive, in order to implement that variably-sized (viz. -sized) nested stack of sum loops that we saw in the pseudocode above. The strategy here is to implement the inner recursive bit (pmf_inner0) as a generator that yields the summands one by one, & then pmf0 does the job of summing them all up with the built-in sum function.
We also have special-casing for when , in which case the starting state () is already converged, so the probability of converging in exactly zero steps is 1, & the probability of converging in exactly steps for any other value of is 0. On the other hand, if and yet , then we cannot possibly converge (as we need at least one step to get from to convergence), so we always return 0 in such cases.
Phase III: Can we go faster?
So, we accomplished something nice: we now have a computer program that will calculate accurately — indeed, with unlimited precision — for any values of and . But I still have three serious issues with what we’ve got so far:
- This implementation is ludicrously slow. Using
pmf0is not recommended unless you just want to laugh at how slow it is. - What I was dreaming of, in my mind, when starting on this problem, was coming up with a nice-looking formula — the kind that you might see in a textbook on, say, probability theory or something. We’re definitely not there yet.
- I also care about some other properties of the distribution. Knowing the PMF is certainly extremely important & effectively defines the distribution, but I also want to know things like the expectation, the variance, &c..
So, let’s tackle these three issues, roughly in the order stated above.
My next iteration on the Python implementation is called pmf1, and it looks something like this:
def pmf1(k, n):
if k == 0:
return Q(1) if n == 0 else Q(0)
elif n < 1:
return Q(0)
return pmf_inner1(k, n, 0)
def pmf_inner1(k, n, d):
denom = 2 * k + 1 - d
if n == 1:
return Q(2, denom)
else:
return sum(
Q(1, denom) * pmf_inner1(k, n - 1, max(d - i, i, d))
for i in range(d - (k - 1), k)
)
As you can see, pmf1 basically looks like pmf0 except that it calls pmf_inner1 instead of pmf_inner0, and it doesn’t sum the results. The main thing that distinguishes pmf_inner1 from pmf_inner0 is that it does its own summation, thus being an ordinary function (which just returns a single rational number) instead of a generator. This makes things more explicit. It also possibly removes some overhead that the generator approach might have, but really I wouldn’t expect it to be much faster — the added explicitness is what’s important.
That brings us to the next iteration, pmf2, which is where we see the real performance gains:
def pmf2(k, n):
if k == 0:
return Q(1) if n == 0 else Q(0)
elif n < 1:
return Q(0)
return pmf_inner2(k, n, 0)
def pmf_inner2(k, n, d):
cache = {}
def f(n, d):
if (n, d) in cache:
return cache[(n, d)]
denom = 2 * k + 1 - d
if n == 1:
return Q(2, denom)
else:
r = sum(
Q(1, denom) * f(n - 1, max(d - i, i, d))
for i in range(d - (k - 1), k)
)
cache[(n, d)] = r
return r
return f(n, d)
That’s right, this is a job for dynamic programming! By memoising already-computed values of f(n, d) (k is a constant for a given invocation of pmf_inner2, so we don’t need to store its values) in a dictionary called cache, we avoid most of the recursion that we would otherwise perform, thus dramatically cutting down the computational complexity of pmf2.
Oh, but we can do even better. As it turns out, we’re actually unnecessarily duplicating quite a bit of work. We did all that reasoning above to arrive at “”. However, there’s actually a similar, but easier, way to look at it. If and we haven’t yet converged, then the next level added to falls into exactly one of three cases: strictly less than 0, somewhere within , or strictly greater than .
Crucially, the number of possible levels in the first case is exactly the same as the number of possible levels in the third & final case — viz. — & these levels are symmetric; we get the same result if we consider adding −1 to as if we consider adding , the same result if we consider adding −2 as if we consider adding , & so on. And adding any level to that’s within yields the same result as adding any other level that’s also within that interval, so we can just do the computation for one particular level, & then multiply the result by the number of possible levels within this interval, viz. .
Just to make things more concrete with an example, consider and . The set of possible levels that could be added to in the next step are as follows (this is computed as ):
We can partition this set into the three cases that we have in mind:
As expected, the first & last sets in this partition both have cardinality , & the middle set has cardinality . In this example, the symmetry is that −1 & 4 are paired, −2 & 5 are paired, −3 & 6 are paired, −4 & 7 are paired, and −5 & 8 are paired. By “paired”, I mean that the result (i.e. the new value of ) is effectively the same, no matter which element of the pair is added to in the next step. So, for example, instead of computing a probability under the assumption that −1 is added to in the next step, & then doing the same for 4, & then adding those two results; we can simply do it for just 4, & then double the result. Furthermore, instead of doing separate computations for every element of and then summing the results, we can just do it for 0, & then multiply that result by .
This gets us the next iteration of our little Python program, which I simply call pmf:
def pmf(k, n):
if k == 0:
return Q(1) if n == 0 else Q(0)
elif n < 1:
return Q(0)
return pmf_inner(k, n, 0)
def pmf_inner(k, n, d):
cache = {}
def f(n, d):
if (n, d) in cache:
return cache[(n, d)]
denom = 2 * k + 1 - d
if n == 1:
return Q(2, denom)
else:
r = sum(Q(2, denom) * f(n - 1, i) for i in range(d + 1, k)) + Q(
d + 1, denom
) * f(n - 1, d)
cache[(n, d)] = r
return r
return f(n, d)
This was about as far as I could manage to refine this function, at least whilst still getting results with unlimited precision. We can go quite a bit faster by switching from Python’s fractions.Fraction to its built-in float datatype, which simultaneously limits our precision to a fixed number of bits (viz. 64 bits), & takes advantage of the fact that modern CPUs contain specialised hardware for working with IEEE 754 double-precision (a.k.a. binary64) floating point numbers. The result is pmf_float:
def pmf_float(k, n):
if k == 0:
return 1.0 if n == 0 else 0.0
elif n < 1:
return 0.0
return pmf_inner_float(k, n, 0)
def pmf_inner_float(k, n, d):
cache = {}
def f(n, d):
if (n, d) in cache:
return cache[(n, d)]
denom = float(2 * k + 1 - d)
if n == 1:
return 2.0 / denom
else:
r = (
2.0 * sum(f(n - 1, i) for i in range(d + 1, k))
+ float(d + 1) * f(n - 1, d)
) / denom
cache[(n, d)] = r
return r
return f(n, d)
Note that this implementation sticks to integer arithmetic wherever possible, only resorting to floating-point arithmetic when absolutely necessary. pmf_float is very usable and gives results of quite good accuracy, as there’s nothing being done here that is particularly numerically unstable. So, it should be preferred over pmf unless you actually need to know the exact rational number for some reason.
Okay, but, how fast is it, really? Oh yes, it’s time for some benchmarks! But only really crappy ad hoc ones, because I’m lazy & there’s no reason to be obsessive about accuracy here…
But first, we need just one more implementation to benchmark: a Rust implementation of pmf_float! I didn’t bother making a Rust implementation of pmf because, again, I was too lazy, & I really just wanted to see how quickly I could compute to an accuracy that’s sufficient for any realistic application. The Rust implementation looks something like this:
use rustc_hash::FxHashMap as Map;
pub fn pmf(k: u32, n: u32) -> f64 {
if k == 0 {
if n == 0 {
1.0
} else {
0.0
}
} else if n < 1 {
0.0
} else {
pmf_inner(k, n, 0)
}
}
fn pmf_inner(k: u32, n: u32, d: u32) -> f64 {
fn f(cache: &mut Map<(u32, u32), f64>, k: u32, n: u32, d: u32) -> f64 {
if let Some(x) = cache.get(&(n, d)) {
return *x;
}
let denom = f64::from(2 * k - d + 1);
if n == 1 {
2.0 / denom
} else {
let sum: f64 = (d + 1..k).map(|i| f(cache, k, n - 1, i)).sum();
let r =
(2.0 * sum + f64::from(d + 1) * f(cache, k, n - 1, d)) / denom;
cache.insert((n, d), r);
r
}
}
let mut cache = Map::default();
f(&mut cache, k, n, d)
}
As you can see, this is pretty much exactly equivalent to how the Python pmf_float function is written, with the slight exception that I don’t use the hash function from Rust’s standard library (std), & instead depend on the rustc-hash crate.[1]
So, uhm, let’s see the (crappy) benchmarks?:
Raw outputs
pmf2: 19.257901867997134
pmf: 7.60964249499375
pmf_float: 0.23313972300093155
pmf(20, 24) time: [50.477 µs 50.482 µs 50.487 µs]
Found 5 outliers among 100 measurements (5.00%)
3 (3.00%) low mild
2 (2.00%) high mild
| language | function | time (μs/iter) | time (relative) |
|---|---|---|---|
| Python | pmf2 |
192 579.02 | 3 814.96× |
| Python | pmf |
76 096.42 | 1 507.46× |
| Python | pmf_float |
2 331.40 | 46.18× |
| Rust | pmf |
50.48 | 1.00× |
The implementations were benchmarked solely on their ability to compute . You’ll notice that I did not benchmark pmf0 nor pmf1, because those implementations lack the memoisation required to run in a reasonable amount of time.
For Python, I used timeit to do the benchmarking (see: bench.py), & for Rust, I used Criterion.rs (see: benches/pmf_benchmark.rs).
You can see the full listings for the Python implementations at rbc.py, and for the Rust implementation at src/lib.rs & src/tests.rs.
Footnotes for “Phase III: Can we go faster?”
-
[↑] As of this writing, Rust’s standard library uses SipHash (specifically SipHash-1-3) by default. This is because SipHash makes use of an ARX structure that makes it highly resistant to hash flooding attacks, thus making it a good default choice if you’re not sure whether the user will need that security.
However, we don’t care about that kind of security in this case, so we can just use rustc-hash to hash things stupidly quickly. If you’re wondering what rustc-hash actually looks like, it hashes a
usize(which is a pointer-sized unsigned integer) at a time, like so (simplified under the assumption that you’re compiling for a 64-bit architecture):const K: usize = 0x517cc1b727220a95; fn add_to_hash(&mut self, i: usize) { self.hash = self.hash.rotate_left(5).bitxor(i).wrapping_mul(K); }Note that
0x517cc1b727220a95= .
Phase IV: Where da formula @, doe?
I regret to inform you that I could not figure out a closed-form expression for — at least, not for a restrictive definition of “closed-form”. Booooo… 😤👎 Embarrassing……
However, it is certainly possible to come up with a recursive “formula” modelled on the programmatic implementations that you see above. This is not a single expression, so it’s not a “closed-form expression”, but it is a fixed number of expressions (really, just two expressions) that are, individually, technically closed-form — at least, by Wikipedia’s definition of “closed-form”, which allows summation, so long as it’s not infinite. Basically, this is the best I got:
As you can see, there are two forms that you can choose from for the recursive bit of : the one on top is modelled on pmf2, & the one on bottom is modelled on pmf. The pmf2-based one actually looks a bit cleaner & less verbose, but of course, we know that it’s computationally just not as good. Plus, we avoid using at all in the pmf-based one, which is nice.
So, that is (or rather, “those are”, as there are two versions) the closest thing that I have to a “nice formula” for RBC. If you’re a better mathematician than I am (frankly, not a very high bar to exceed…), & can figure out an even nicer formula, please please do let me know about it!
To get an idea of what looks like, we can plot it! Check out this plot that focuses in on just the first 15 values of :
(This, & other plots shown here, were created using matplotlib; see plot.py.)
Cool!! I’ve used cubic Hermite spline interpolation to show a smooth curve that fits all 15 points, but do remember that this is a PMF, not a PDF! There are really only 15 points (probability masses) here, & the smoothed curve is just there to guide your eyeballs.
To get a bigger picture than this, we can consider the first 100 values of instead of the first 15, & we can consider multiple values of , as well:
🤩 Wowww… Pretty~
You can see that this distribution gets real flat-like for larger values of . For , it nearly looks like a damn linear function with a mildly negative slope!
Phase V: How do I know what to expect?
So, we have a PMF. But we also want other nice things, like the expectation of that PMF. How in the damn hell am I supposed to figure that out?
Well, I decided that estimating the expectation was a good start. So I wrote a little Python function to do just that:
def estimate_expectation(k, epsilon):
e = 0.0
cumu_prob = 0.0
n = 1
while cumu_prob < 1.0 - epsilon:
prob = pmf_float(k, n)
old_cumu_prob = cumu_prob
cumu_prob += prob
e += prob * float(n)
n += 1
if old_cumu_prob == cumu_prob:
break
return e
The idea here is very simple: for a given value of , we calculate , , , & so on, keeping track of the sum of the probability masses that we’ve calculated so far. For each such calculation, we add to our running total, & then return that running total when the sum of the probability masses that we’ve calculated so far is sufficiently close to 1.
What does “sufficiently close” mean? Well, that’s determined by the value of epsilon (); we just need to get to at least . I used sys.float_info.epsilon for the value of , but the basic idea is that larger values of will give less accurate results more quickly, & vice versā.
By running estimate_expectation for the first few values of , I got something like this:
[
0.0,
1.4999999999999991,
2.2499999999999845,
2.9166666666666576,
3.541666666666626,
4.141666666666597,
4.724999999999947,
5.296428571428546,
5.858928571428415,
6.414484126984054,
6.964484126984016,
7.509938672438514,
8.051605339105192,
8.590066877566773,
9.125781163280985,
9.65911449661434,
10.190364496614361,
10.719776261320147,
11.247554039097999,
11.77386982857149,
12.298869828571545,
12.822679352381105,
13.345406625108346,
13.867145755543156,
14.387979088876463,
14.907979088876447,
15.427209858107194,
15.945728376625619,
16.46358551948275,
16.98082689879308,
17.497493565459727,
18.013622597717774,
18.52924759771753,
]
Naturally, these are just estimations, so we expect them to be a little bit off the mark — specifically, a little bit lower than the true value. Nonetheless, this level of accuracy was enough to see some clear patterns. I decided to take the difference sequence of these estimations, essentially calculating estimations of , , , & so on (…where is the expectation operator). I then went through this sequence, by hoof, & for each difference in the sequence, I wrote down which rational number it looked like it was estimating. For example, 1.4999999999999991 looks like it’s estimating . The result was this:
As it turns out, the first element in this sequence () is a red herring — it results from the fact that we’ve defined to be 0 for any value of . By ignoring this first term, I could see that the terms in this sequence are just , with the exception of the value for being by fiat. It was this knowledge that I was able to come up with the expected value for :
In this context, “” means that is a random variable that has as its distribution. I’ve called it “” because the concrete values that it takes on are values of , i.e. exactly how many steps it took us to converge.
Below the horizontal line, I show an equivalent formula that apparently isn’t recursive, & thus looks like a closed-form expression for . However, denotes the th harmonic number, which itself doesn’t have a closed-form definition in the strictest sense of “closed-form” — there’s just the usual “partial sum of the first terms of the harmonic series”, which may or may not be a closed form, depending on whom you ask. 😉
In any case, there is a really really (like, really) good approximation for that is most definitely closed-form, which I used to come up with the approximation that you see after the “”. The “” stands for “natural logarithm”, and is the Euler–Mascheroni constant (). I’ve also used big notation to express that asymptotically grows as — that is, linearly.
If you want to know just how good this approximation is, feast your eyes:
Soooo… yeah. It’s basically indistinguishable from the true value at or so… If you’re wondering what’s up with the random singularity that appears in the plot of the approximation, that’s due to the term, which comes from a truncation (yet another partial sum!) of the Taylor series representation.
Also in rbc.py, there are implementations for calculating the exact expectation…:
def expectation(k):
if k == 0:
return Q(0)
e = Q(3, 2)
for i in range(2, k + 1):
e += Q(i + 1, 2 * i)
return e
…And the same thing, but using floats…:
def expectation_float(k):
if k == 0:
return 0.0
e = 1.5
for i in range(2, k + 1):
e += (i + 1.0) / (2.0 * i)
return e
…As well as for the approximation:
from math import log
GAMMA_PLUS_1 = 1.577_215_664_901_532_8
def expectation_approx(k):
if k == 0:
return 0.0
k = float(k)
return 0.5 * (k + log(k) + GAMMA_PLUS_1 + 1.0 / (2.0 * k))
Phase VI: How do I know what not to expect?
Okay, so we know the expected value of , which is great. But what about other nice statistical properties? Like…
Variance
…The variance? Once again, I’ve no clue how I’d go about finding this analytically, so we’re going to once again resort to estimations.
The variance can be expressed as simply the expectation of the square of the value, minus the square of the expectation of the value. Symbolically:
Using this equation directly in computation — when using floating-point arithmetic — can be quite numerically unstable, but we’re gonna do it anyway, because I don’t think that we’re gonna have that issue (particularly, because it seems like is quite large).
Thus, we can use the same strategy that we used for estimating the expectation to approximate :
def estimate_expectation_sq(k, epsilon):
e = 0.0
cumu_prob = 0.0
n = 1
while cumu_prob < 1.0 - epsilon:
prob = pmf_float(k, n)
old_cumu_prob = cumu_prob
cumu_prob += prob
e += prob * float(n * n)
n += 1
if old_cumu_prob == cumu_prob:
break
return e
Then, it’s easy enough to straightforwardly compute an approximation of . I did this, & I unfortunately could not find an exact formula for the results. Instead, I fiddled around with some approximations — using quadratic regression provided by NumPy as a starting point — & ended up with this:
🤷🏽♀️ Sure, why not. It looks nice. And it seems to be a pretty solid approximation! The major takeaway here is that is very much quadratic in , which makes sense, as we expected the variance to be quite large on the basis of those plots of that we saw above. Note that this is very comparable to the variance of the uniform distribution, which is just , where is the support of the distribution. Whew… that’s really saying something!
Median, mode
What about the median? The mode? Both of these can be calculated. For the median, you can do something like the estimate_expectation function above, except you don’t have to keep a running “expectation” (e) total, & you simply stop as soon as the cumulative probability is 0.5 or greater. For the mode (which is just the peak of the distribution — for a given value of , this is the value of that maximises ), you can do something like:
def mode(k):
p = 0.0
n = 1
while True:
prob = pmf_float(k, n)
if prob > p:
p = prob
else:
break
n += 1
return n - 1
We know the shape of the distribution, so we just wait for it to start decreasing, & we know that we’ve already seen the mode.
I didn’t go any further with these two measure of central tendency, as I was very much not confident in my ability to find some pattern… In any case, here’s a table of some modes, if that makes you feel any better:
| mode | |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 5 |
| 3 | 13 |
| 4 | 26 |
| 5 | 45 |
| 6 | 70 |
| 7 | 103 |
| 8 | 142 |
| 9 | 188 |
| 10 | 242 |
The values here are the absolute lowest values for which the mode is as listed.
Entropy
What about the information entropy[1] of this distribution?
If you’re not already familiar with the idea of entropy, the basic idea is that less likely outcomes carry more “surprise” or “information” with them. A simple example might be if you got a single bit sent to you (say, via telegraphy) every 24 hours that indicated whether it was raining in a particular locale. If that locale is considered to be arid, then most of the time, you’re gonna get a “not raining” message. Thus, getting a “not raining” message gives you very little information; you’re not very surprised. On the other hand, on the occasions when it does rain, & you get an “it’s raining” message, that’s a lot of information & surprisal — you wouldn’t’ve guessed that it was raining, had you not gotten that message. If we have an idea of the probability for each outcome (for “not raining” & for “it’s raining”), then we can calculate the amount of information/surprisal that we get from a single telegraph message in general, without knowing the actual contents of the message — it’s just the expectation of the surprisal (i.e. the surprisal of each outcome, weighted by the probability of that outcome, all summed together).
What’s the “information content”[1] of a particular outcome? Well, as it turns out, it’s basically just , where is the probability of that outcome.
If you’re wondering what in the gosh darn’d heck logarithms have to do with this, one thing that can help it make intuitive sense (if you’re like me & have computer brain) is thinking of bit-strings: a bit-string of length has possible values, so to go the other way (from to ), you’re gonna have to undo that exponentiation… with a logarithm. In particular, if we have — for example — a uniform distribution over all possible values of the bit-string, then the probability of any one outcome is . Then, for any , .
In any case, we can again use the same technique that we used for estimating & for estimating to estimate . (Note that the “” in “” is an uppercase Greek letter eta (U+0397), not an uppercase Latin letter (h)aitch (U+0048); the “” stands for the initial ⟨e⟩ in the word entropy.)
Here’s a Python function that does just that:
import math
def estimate_entropy(k, epsilon):
eta = 0.0
cumu_prob = 0.0
n = 1
while cumu_prob < 1.0 - epsilon:
prob = pmf_float(k, n)
old_cumu_prob = cumu_prob
cumu_prob += prob
try:
eta += prob * math.log(prob)
except:
pass
n += 1
if old_cumu_prob == cumu_prob:
break
return -eta
I did something similar to what I did with , except this time, I had no automated regression to help me out. I probably could have written something by hand to assist in this procedure, but I honestly wasn’t sure quite what I was looking for. So instead, I literally just tried some approximations & visually looked (on a plot) at how they compared to the estimated values of , & then did adjustments by hoof as I saw fit. The result is this halfway-decent approximation:
Sooo… yep. I was debating over the use of the “” term, & ended up deciding to use it. Regardless of this term, the result is asymptotically logarithmic in .
Let’s have a look at how good this approximation is:
Eh. It’s alright, I guess. 🤷🏽♀️ I’ve got two y-axes for ease of reading; the one on the left is in nat (nats), & the one on the right is in Sh (shannons; the information-theoretic analogue of the bit).
Footnotes for “Entropy”
- [↑] See also: Information content.
I don’t think that any of that is going to help us clear Pianus…
So, there you have it. Noöne asked for any of it, but there it is. You’re very welcome. 😌
If, for some godforsaken reason, this actually interested you (seems highly unlikely to me, but then again, what do I know about probability?), I’ll just note that there’s more that can be done. could use a better formula, maybe. An exact formula for and/or — or better approximations — would be nice. Maybe a formula for the median and/or mode… Plus, you can consider other related distributions. For example, how is the value of distributed, given a value of both & ?
Have fun! :3
Habyte maketh no monke, ne vvearynge of gylte ſpurres maketh no knyght
With this 2022 Anniversary–Summer event, I — as usual — took a look at the unique hairs, faces, & NX equipment offered by the new event. The way that it usually goes is:
Hmm, none of these faces look like MapleStory faces. I guess these are all from, like, MapleStory version three thousand or something…? That’s too bad… To be honest, I don’t really like any of them.
None of these hairs really look good to me either. Well, I admit that that one seems like it could be pretty cute, but it’s really not my style. Plus, what’s with all of the hairs looking super washed out? They all look white no matter what colour they are…
At least some of these NX equips look neato. Maybe I’ll get a few… maybe do a few wardrobe changes on a character here or there…
Well, this event actually came with two faces that I did kinda like: the Charming Face and the Calm Lucid Face (specifically, I had in mind the female versions, although the male versions are only subtly different). And furthermore, this event came with a hair that I really like: the Balayage Hair (again, specifically the female version; in this case, the male version is completely different)! So, I thought hard about it, and I decided that I wanted to give my woodsmaster capreolina a makeover!! After a lot of fiddling around in maples.im and getting some useful opinions from Lv1Crook (Level1Crook, Lvl1Crook, xXCrookXx) and Harlez (VigiI), I came up with a look, and grinded out Summer Points to get it…:
👀

Cute, right??? For this image, I’ve specifically chosen the Kandiva to match the red eyes, shirt, facepaint, and the kinda reddish highlights.
I had a kinda “left over” look from my experimentations that led to capreolina’s new look, and I was really satisfied with how I felt about giving capreolina a new look. So, I was emboldened to do the same for my pure STR bishop cervid…!:
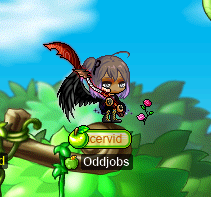
YAY I LOOK ADORABLE LOL
I originally was going to use a different cape, and then realised that the one that I had used in maples.im (which I thought that I remembered checking for in-game) was only purchasable with donor points… and I didn’t have any. Oh well. This cape is cool too.
I think that both of these looks do a pretty good job of preserving the original “vibes” that I was going for with these two characters’ outfits: cervid still has the dark “goth” vibe, and capreolina still looks like she either lives in a tree, or could chop a tree down with her bare hands. However, in another sense, the tables have turned: capre now looks gayer than cervid, instead of the other way around!! In any case, these are my original two characters, so I think that it makes sense for them to both have the same hair style :P
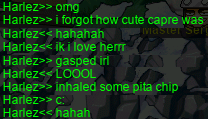
Some other people have agreed that the new looks are cute:
However, the reception has not been entirely positive…:
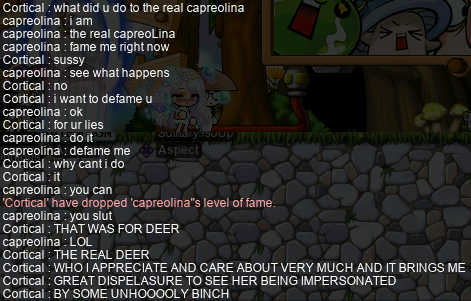
Rest assured that I am the real deer, and I may dress myself however I please!! So there!!!
What hath Dunas wrought!
Over in Neo Tokyo, on my darksterity knight rusa, I did some Bergamoting with marksman xBowtjuhNL, paladin aWildLynux, and bishop Pebbytan:

Afterwards, I trioed D’una with them (minus aWildLynux):

This was rough. D’una is already a massive pain in the ass for me, as a melee attacker, thanks to his insistence on constantly dispelling (DPing) anyone within melee range, and frequently stunning, super-knockbacking, Darkness’ing, etc.… And zerking doesn’t exactly make it easier to survive DR consistently…! But it’s also not so easy for bishops either, despite the fact that they are mages and are thus unaffected (barring STR mages & the like) by physical damage reflection (physical DR). Bishops have to get close enough to Dispel D’una’s pesky buffs (particularly the WDEF ones…), and yet this puts them within D’una’s DP range, thus endangering them by possibly DPing their Magic Guard. As a result of all of this, our first run was a failure: both Pebby & I died. 😭 We did better on the second time around, though. (:
Did you know that it’s possible to get up into the branches of the tree at the Forest of Oblivion (the map that connects the Mushroom Shrine to Kamuna)?:

Yep! And it requires ≥123% JUMP — and thus exactly 123% JUMP, as that is the maximum possible JUMP.
I also did Bergamot with bowmaster xRook (misandrist), who had never done Berga before! We were accompanied by fellow bowmaster OliverQueen and shadower Harlez (VigiI). During the beginning of the first body of the first run, we had xRook crouching and watching so that they would see what Bergamot’s DP animation actually looks like:

Getting DP’d is potentially a big hazard for xRook, as they rely on my HB to survive. Of course, any time that Bergamot does the laser DP animation, I’m always watching very intently to see if anyone does get hit by the smol laser (the one that actually DPs), so that I can quickly rebuff them — which often involves quickly mounting and running to the left, so that I’m within HB distance of them after they get knocked back by the laser.
With that, xRook got the hang of it, and was able to survive the whole run, without the assistance of any bishops!:
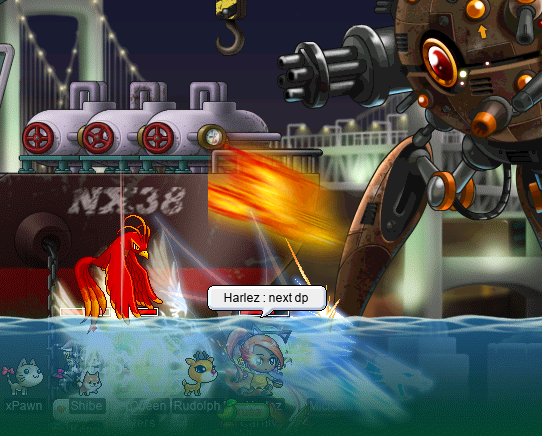
I also duoed Berga, with xBowtjuhNL…:

It actually wasn’t so bad; we didn’t have any serious hitches, and the run took around ≈55 minutes in total. The drops didn’t quite make it worth it, but I guess they were okay — Shield for WATK 70% ain’t half bad (we were both 5⧸5 on cards already):

I also did a trio Nibelung run with xBowtjuhNL and Harlez. xBowtjuhNL said that this was going to be his last run before going to bed, and indeed, he fell asleep during the run…:
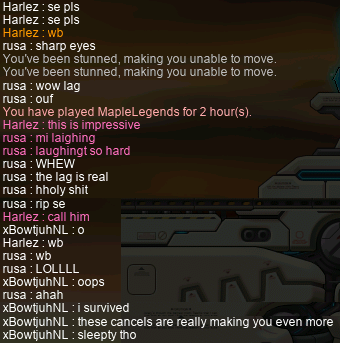
Eventually, as you can see, I was able to wake him up by calling him on Discord™! You can also see that I was having some pretty nasty networking issues at the time…
In the end, though, it was a great run! I levelled up to 173~!:

And Nib was kind enough to drop an EP for us!!:
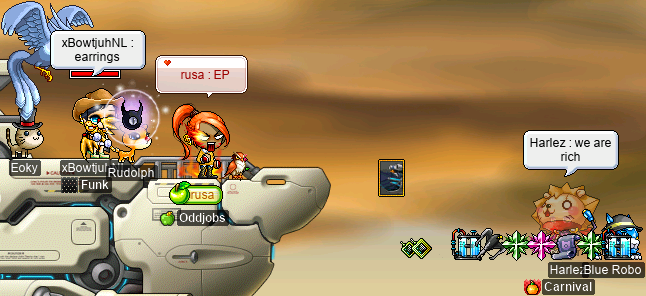
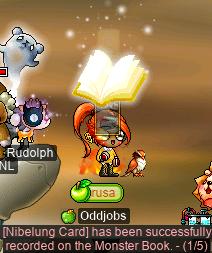
Plus, I got my first Nib card (:
With the splits from selling the EP — which I got from Harlez in pCoins, rather than in mesos — I was able to make another Chaos Scroll, so that I could give another shot to that 4 WATK, 4 slot PGC that I made in the previous entry…:

Oh. Well, that’s a 0 WATK PGC. Maybe next time…… 😢
Swiftness is the essence of warfare
I have procrastinated long enough on getting a Silver Mane for my woodsmaster capreolina. The Silver Mane quest ain’t easy — and it ain’t cheap, either — but the only pre-requisites are being level ≥120[1], and already having the Hog, both of which capreolina has satisfied for… well, like 22 levels now. So, I headed out into the wilderness of the Minar Forest with fellow fourth-job archer Level1Crook (Lvl1Crook, xXCrookXx) to collect the 600 Rexton Leathers, 400 Wooden Shoulder Pads, and 400 Skull Shoulder Pads that we each (yes, that’s 2 800 big fat Leafre ETC items in total!) needed for our respective Silver Mane quests:

Oh, I died. How embarrassing…
Well, I was already pretty close to levelling before we started, so it was no surprise when I levelled mid-grind!!:
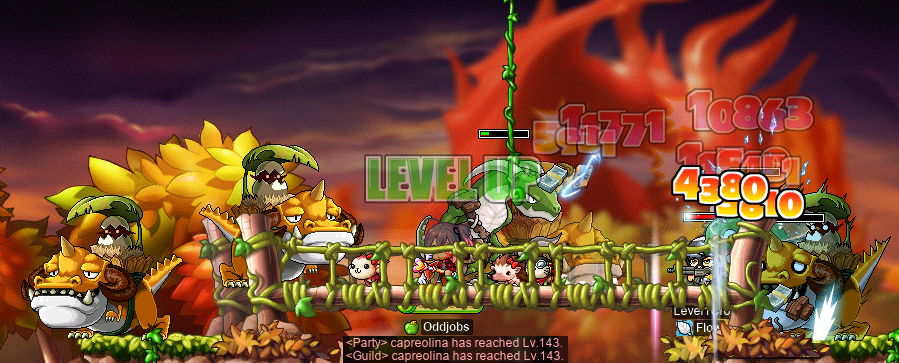
After getting our 1.2k Rexton Leathers, we headed to The Hidden Dragon Tomb II for the rest of the ETCs:

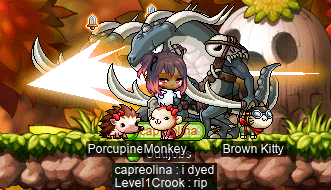
I dyed… again… how embarrassing… Now, I’m not going to say exactly how many times that I died, but I will say that whoever runs the “Cash Shop” was very happy about their Safety Charm sales on that day…
Not gonna lie, 2.8k big Leafre ETCs is way too fucking many. We almost called it a day after we had just a few hundred ETCs left to go, but we agreed to just trudge on and get the entire damn thing over with. The result was that we both suffered mild brain rot that we may, or may not, ever recover from. But we did it. We got the things.
Of course, there was also the issue of getting 50M(!) mesos. For mine, I decided to just steal transfer 50M mesos off of my vicloc dagger spearwoman d34r. And with that, we were now officially Fast As Fuck™:

NYOOOOOOOOOOOOM…
Footnotes for “Swiftness is the essence of warfare”
- [↑] As of this writing, the Silver Mane quest in MapleLegends is bugged, so this is not strictly true for the MapleLegends implementation. As far as I know, the MapleLegends implementation (again, as of this writing) has no level requirement at all, and is instead gated on the PC’s class: namely, they must be a fourth job class, or a beginner.
A clock; a cursèd tree; a cryptid; a character of evil; a captain.
I did a few fun all-odd Capt. Lat runs on my darksterity knight rusa with STRginner extraordinaire Taima (Girlmoder, Boymoder, Nyanners, Tacgnol, Hanyou), helping to HB permabeginners Cortical (GishGallop, Medulla, SussyBaka, RedNurJazlan, CokeZeroPill) and uayua (2sus4u, hueso, shadowban, tb303):
A grandfather clock; a Guatemalan statue; a great foot; a god; a ghost pilot.


Welp, we had some deaths, but that’s to be expected when you’re constantly on the brink of being two-shot by a stray ranged attack from the ol’ Captain.
I also did a single duo Peppered Lattice run on my I/L archmagelet cervine, with marksman Level1Crook (Lanius, Lvl1Crook, xXCrookXx), in which I did some… I don’t know, pretty okay CL damage? To Papal Lettuce? Next time, I’ll have to use some actual MATK potions 😅

That being said, the amount of AVOID that I get from being a magelet really helps when fighting bosses like this; I pretty much stayed on the top platforms for the entire run, so I never got dispelled (DP’d) even once!
We also teamed up with PoultryWoman (Yoshis, Furbs, SwordFurb) and SaviorSword to do some Ravs (with me as my pure STR bishop cervid)…:

…And some Peppy Laters (with me as my woodsmaster capreolina):

And, with marksman xBowtjuhNL and shadower Harlez (VigiI), we did some fun Poppy Lanterns…:

…During which, Taima took advantage of her @roll 100 for loot order being the highest by… looting the one “““dilk””” that dropped:

🤷🏽♀️
And, finally, when swashbuckler Yoshis hit the big level 115, it was time for her to try Ravving, too (featuring F/P archmage 2sus4u)!:

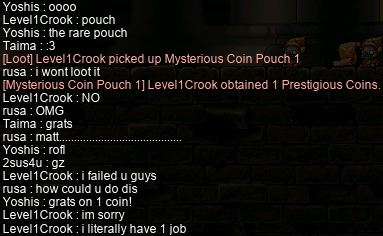
SMH my head… I cannot believe this… How could Level1Crook do this to us?? He was our only MCP-opener……
On cervid, I also helped out xBowtjuhNL, OliverQueen, BeMyRavebae, BimboBucc, and atsumoo sell some AFK zhelms!:

It was a little weird not being the only active bishop in the party, but it worked out well enough:

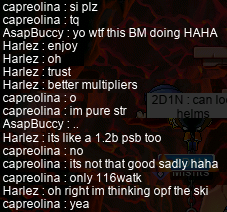
I also did some Zakking on capreolina, where — as usual — I got some weird looks when I bust out the ol’ PSB for the arms stage:
I also did an… interesting Zak run on rusa, wherein we lost our bishop and bowmaster quite early on during the arms stage, leaving just me, Harlez, nightlord Peeko, and paladin SirAmik… And then SirAmik died during the first body. So, yeah, it was kinda a trio Zak without even so much as SE:
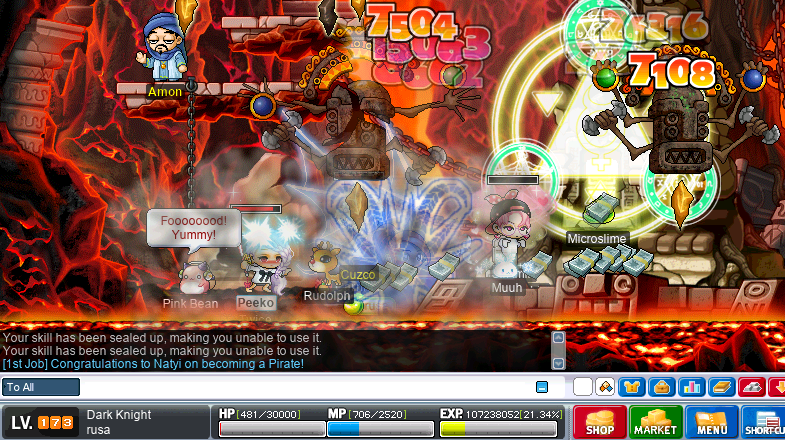
So, yeah, that was pretty brutal. And by the end of it, only one third (⅓) of our original party remained 😆:

And still, no pouch… 🙄
Acer
Over on Maple Island, I was killing some Zombie Lupins on my islander ozotoceros:

…Wait, what? Oh, right, that’s BRPQ (Boss Rush Party Quest; BPQ), not Maple Island. Naturally, the Faust inside of BRPQ spawns zlupins just like the ordinary Faust does, so it’s a favourite pastime of islanders during every summer event to try to squeeze a Red Whip out of one of ’em…
Unfortunately, the Red Whip drop rate is not great, so I didn’t get any. :P But I did get a fancy Dark Pilfer! And some Cursed Dolls…
In any case, I did amass enough anniversary points to purchase myself a fancy-dancy claw: the Sweet Fork Cake!!:
And, after a sufficient amount of prayer directed at the Maple gods, I was blessed with a set of Maple Throwing-Stars that I got from a Maple Equipment Box that I bought with more anniversary points!!!:
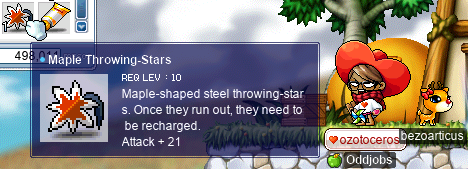

For those not aware, Maple Throwing-Stars are extremely valuable on Maple Island, which may come as a surprise given that they are virtually worthless elsewhere. The extra +6 WATK over what you’d get from Subis makes a huge difference (as your total WATK is naturally low anyways), and it’s not like there’s any way to get Ilbis on Maple Island…
Oh, and I hit level 46~!!:

The raffle loves giving me useless equipment like Maple Guns, Maple Crows, and most of all: Red Bandanas.
🤦🏽♀️
And, of course, you know I finished all five weeks of DJ JM’s quests! So I walked away with my chair of choice…

I’ve seen some people in alliance chat hating on my homegirl Pia, and all I have to say is that Pia is the O.G. Pia has been in Henesys Park since before y’all were even old enough to operate a keyboard, so put some damn respect on her name!!
A squamate appears
As teased in the previous diary entry (which I started writing before I actually turned in the corresponding quest), I got the next Monster Book Ring tier for my darksterity knight rusa: T4!

And just in time for another Horntail run!:

Our nightlord Brokeen accidentally entered the main body map just a fraction of a second earlier than shadower Harlez (VigiI) — our intended seduce target — which is why you see him dead in the above image.
Unfortunately for me, I got what I asked for by screenshotting someone else’s death, and a later screenshot caused my client to crash when all three heads were still alive. ☹️
You can see corsair runYoShit in the screenshot above, which is notable because runYoShit was relying on my HB to survive, so my crashing meant that they didn’t get to continue the run either!! 😭
In spite of this, I nevertheless signed up for the next run that xBowtjuhNL hosted, mistakenly believing (not without reason) that the screenshotting was what caused the crash — after all, the crash happened instantaneously after hitting the Prt Sc key, which activates the client’s built-in screenshotting ability (which regrettably cannot be unbound from said key):
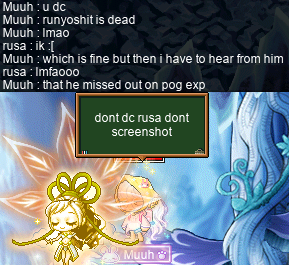
So, true to my word, I did not screenshot. And, in spite of this, I crashed at the beginning of the main body fight anyways…:

This really took the wind out of my sails, as I was not only saddened that I couldn’t HT anymore (as I quite like HTing, and it’s good EXP to boot!), but was also ashamed that I had let down runYoShit on more than one occasion as a result of my own technical issues effectively killing them. I posted about these technical issues, and some related ones, that are associated with the 2022 Anni–Summer event patch — and that I could confirm were not unique to me, i.e. I was getting multiple identical experiential reports from other players — in a MapleLegends forum post entitled “Client crashing/stability/UB issues since Anni–Summer event patch”. Unfortunately, w.r.t. the specifically crashing issues, the client appears to be unwilling to emit crash logs, so the reports that I give are purely phenomenological.
I’ve even desperately attempted to run the game client natively on Windows™ via multi-booting, just for the purpose of not crashing in crash-y situations (read: Horntail). I know, I know, Bill G8s owns my computer now and probably knows all of my deepest darkest secrets, BUT I REALLY WANT TO HT, OKAY‽‽‽ Plus, I always make sure to wash my hooves after using Windows™. :] Unfortunately, it seems that running the MapleLegends client on Windows™ is even crashier than running it in Wine on Linux like I normally do — I don’t even have to go into HT (nor do anything special, really…) to crash! But I’m not terribly surprised, considering that running ML in Wine has always had a much better track record — for me, at least — than it’s had for those running the game natively.
Dark doubts between the promise & event
As the 2022 Anniversary–Summer Event has continued, I have continued BRPQing — including a pair of BRPQs that I did on my vicloc dagger spearwoman d34r, alongside STRginner Cortical (GishGallop, Medulla, SussyBaka, RedNurJazlan, CokeZeroPill). We fought Franky, everyone’s favourite PQ boss:

And I then realised my limitations when our party arrived at Manon, and I could scarcely hit the damn thing — it’s 19 levels higher than me, and has 39 AVOID!:

Good thing Manon isn’t real and Leafre is a hoax perpetuated by so-called “fourth-jobbers”, so I don’t have to worry about it outside of BRPQ.
On my darksterity knight rusa, I did enough BRPQs and Maple Syrup’d enough Maple Leaves to make a pretty awesome one!:
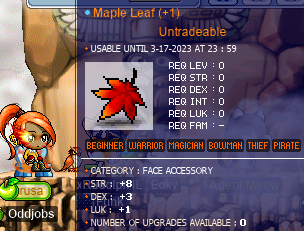
8 STR and 3 DEX on a face accessory? Yell heah!!
I also ended up doing a number of solo BRPQs, as a result of underwhelming traffic at BRPQ around the times that I was logging on. Like on my I/L archmagelet cervine:

And on my daggermit alces:

Unfortunately, both of them ended up wasting most of their points on failed Maple Leaves… But cervine still has a usable clean one, so that’s good, at least.
Oh, and I did manage to get just one (1) good raffle between my two viclockers: a Rabbit Lamp Chair!!:

Normally I really couldn’t care less about chairs (other than their value on the market when I rid myself of them), but I do enjoy getting chairs on my area-restricted characters, i.e. my islander and my viclockers. :]
绝密
绝密
An ongoing investigation into ██████ █████████ by the name of ███████ found ██████ █████ ████ ██████████████ in addition to █████████ activity near the 101st floor of the Eos Tower, where the subject was reported █████████ ██████████████ ████, although █████████ ████████:

█████████ ██████████ ███ █████████ ██ and — it is suspected — █████████ ██████. ██████ agents █████████ and ███████ were reported dead after ████ █████████ █████████████ ███ and attempting reconnaissance on the subject:

It should be reiterated that the subject is armed & dangerous, and only ████████ agents with high levels of clearance, training, & expertise are allowed on this case. It should also be noted that █████ ███ █████████████ ████ ████████, with ████████ ██████ and access to highly advanced technology, including ████████ █████ and ████ ████████ ██ appears to be some kind of temporary invincibility, pending further investigation:

Concerningly, the subject █████ ████████ ██████ ███, gaining access to the highly restricted █████████ ██████ ██████████ Eos Tower spire, where ██████ ██████ killing ████████ and ███████ (nippled clockwhale specimen):

CURRENT STATUS: TOP PRIORITY. ALL DISCRETIONARY RESOURCES ARE TO BE DEDICATED TO THIS CASE.
R. t. tarandus
As usual, it’s time for a quick episode of everyone’s favourite series involving a pugilist whose name starts with a ⟨t⟩ and ends with an ⟨s⟩: Questing With tara™!
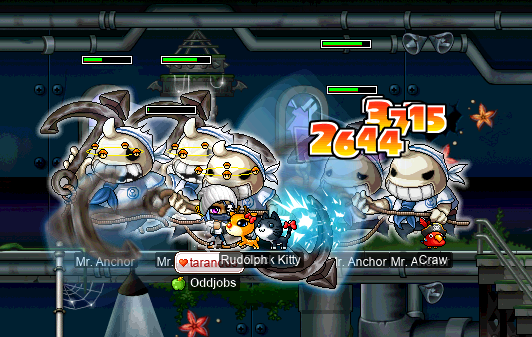
This time around, I headed to Singapore to do some more Capt. Latanica prequests, now that I was high enough level to continue them. I got the necessary Selkie Jr. and Slimy kills at MP3…:

…And the necessary Mr. Anchor kills at GS6:
With that, I was now at the final part of the questline: to slay Capt. Latanica and bring back his Black Essence. Knowing that I wouldn’t have accuracy issues due to Capt. Latanica’s abysmally low AVOID, I decided to just give it a shot and try soloing the Captain:
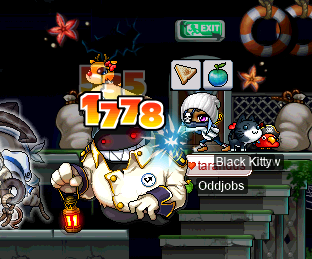
By the end of it, I had used three Unripe Onyx Apples and one Maple Music Fever, and… well, I decided against wasting more resources & time getting irritated at how little damage I was doing to Lat. Could I have finished? Sure. There’s no timer, so I could just eat all of my resources and chip away endlessly at Lat until he finally submitted to my unending patience. But I wasn’t really willing to do this unless I brought some full-blown Onyx Apples with me, so I bailed. I figured that it would have been easier, given that Lat has “only” 700 WDEF, but I neglected to take into account Capt. Lat’s 37-level advantage. 🤦🏽♀️
Of course, not only was this a waste of the WATK potions that I used, but it was also a waste of the White Essence that I got from “The great secret reveals”. But that was okay, because I needed to do The Lost White Essence anyways — for the question completion, if nothing else. So I grinded some more GS6 to finish that quest, and got my White Essence back.
The problem was that, now that I’d done The Lost White Essence, actually successfully soloing Capt. Lat would give me enough EXP to level up! And how tf am I supposed to wear my INTelligent pyjamas if I’m soloing the Captain?? 🙄 So I decided on the “level up, and then come back” route, even though it would mean soloing Capt. Lat at level 64 at the lowest, rather than 63 as I had originally planned (as 63 is the absolute minimum level to have the Capt. Lat kill quest active). So, it’s not as cool, but whatever. I’m still slightly torn on whether or not I should come back with some Onyx Apples at level 64 to solo this big guy. It’s kind of stupid & a waste, but “doing conventionally inadvisable things because I can” is kind of a running theme of my diary, so, you know… Let me know if you have an opinion on the matter…
In any case, for the whole levelling-up thing, I decided to start on the MLG[1] quests. So I headed to Mu Lung to punch some STDs (not to be confused with STDs) for No Gong’s Teaching:
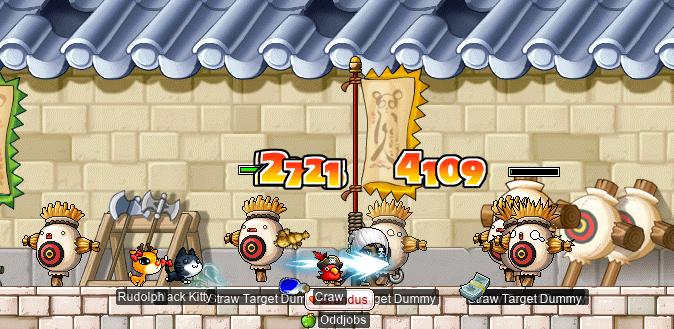
And, welp, that was enough for level 64~!:

I also took a detour to Victoria Island to do some Evil Eye slaying for the latter part (the 999-kill quest) of POLLUTED! ⟨1—Evil Eye⟩, alongside Vicloc I/L gish VigiI (Harlez):

Tune in next time, to Questing With tara™, to learn the fate of the captain known as “Latanica”……
Footnotes for “R. t. tarandus”
- [↑] “Mu Lung Garden”, the region that encompasses all of the Mu Lung and Herb Town maps.
The Room of the Guilty
And, finally, I did one (1) OPQ. On my OPQ mule, sets. With DEXginner inhale (DexBlade, vork) and disgraced[1] former Viclocker Lanius (Level1Crook, Lvl1Crook, xXCrookXx). After a great deal of struggle within the Tower of the Goddess, we killed Father Pixel, with the assistance of an aubergine dressed as a human by the name of AgentPewPew:
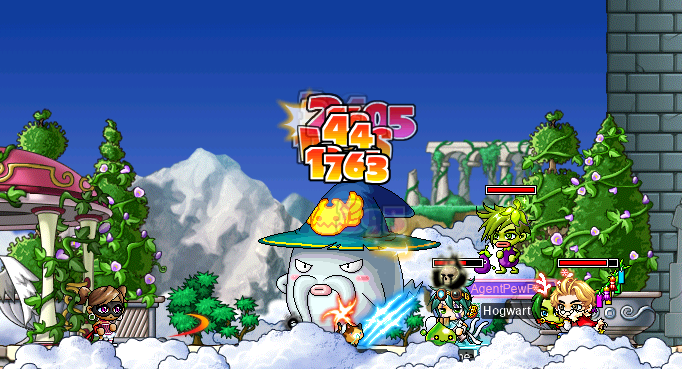
The random folx (including AgentPewPew) that we’d partied with were obsessing over my damage and equipment (which is almost entirely borrowed from my other characters…), but I was more interested in inhale’s damage (see “Comparing DEXginners” in the previous diary entry).
In any case, it was in this PQ that inhale hit the big level 70~!! Oh — and I also levelled up, to 67 :]
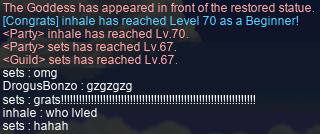
…And then I passed tf out. 🛏️😴💤
Footnotes for “The Room of the Guilty”
(…cnvpstdf…)
cnvpstdf
![]()

This diary entry is dedicated to Pebbytan, who was permanently banned from MapleLegends without possibility of appeal, without having broken any of the rules of the server, merely through guilt by association. ❤️
