rangifer’s diary: pt. lxii
Taxonomising odd jobs, pt. iii: Exploring the space of possible taxonomies. §4
In the previous section of this part (pt. iii, §3), I talked about some clustering methods, including neighbour-joining, as well as linkage-based hierarchical clustering methods. The latter methods need some way of determining linkage; we called these linkage criteria. There are more linkage criteria out there than I care to talk about, but there is just one more that I want to go over, in addition to the ones in §3:
Energy distance
The energy distance, as a linkage criterion, can be thought of (if you squint just a little bit) as a more sophisticated version of UPGMA (see §3). As its name implies, it is actually a full-blown metric (sOmETiMEs), which is nice. Defining the energy distance is not all that complicated, but because its origin is in defining (statistical) distance between probability distributions, I want to start with that kind of definition first.
Between real-vector-valued probability distributions
Let 𝐯, 𝐯′ ∈ ℝ𝑛 be random vectors[1] each with distribution function 𝒱, and let 𝐰, 𝐰′ ∈ ℝ𝑛 be random vectors each with distribution function 𝒲. Let {𝐯, 𝐯′, 𝐰, 𝐰′} be independent. Then the square of the energy distance between 𝒱 and 𝒲 is defined as follows:
𝐷2(𝒱, 𝒲) ≝ 2 ⋅ 𝖤[‖𝐯 − 𝐰‖] − 𝖤[‖𝐯 − 𝐯′‖] − 𝖤[‖𝐰 − 𝐰′‖].
It may be alarming that we have subtraction going on here, as this is the square of the energy distance, so to recover the energy distance itself, we have to take the positive square root. If the squared distance is less than zero, we will end up with an imaginary result, which we obviously cannot tolerate for a distance function. For the definition above, where we are talking about independent real random vectors, and comparing their respective distributions, it works out (for the same reason discussed below). However, it is common to generalise the energy distance to arbitrary metric spaces (which is basically what we want to do here). Before worrying about 𝐷 being a metric in the general case, here is the general case itself:
Any metric space, not just real coordinate space
Let (𝑀, 𝑑) be a metric space. Treat 𝑀 as a sample space[2], and let 𝒜, ℬ both be probability measures over it. Let 𝐚, 𝐚′ ∈ 𝑀 be random variables each sampled from 𝒜, and let 𝐛, 𝐛′ ∈ 𝑀 be random variables each sampled from ℬ. Let {𝐚, 𝐚′, 𝐛, 𝐛′} be independent. Then the square of the energy distance between 𝒜 and ℬ is defined as follows:
𝐷2(𝒜, ℬ) ≝ 2 ⋅ 𝖤[𝑑(𝐚, 𝐛)] − 𝖤[𝑑(𝐚, 𝐚′)] − 𝖤[𝑑(𝐛, 𝐛′)].
It’s not really important to understand the details of this more general definition (or of the original definition, for that matter…), but I’ve taken Wikipedia’s definition here, and cleaned it up so that my head doesn’t hurt when I read it. As you can see, it looks basically like the first definition, except that the leading text is worded a little differently. This definition will lead us to the actual definition that we care about.
In general, this 𝐷 is a metric iff 𝑑 is something called a strict negative definite kernel (Wikipedia calls it a strongly negative definite kernel). This term is defined in a 2005 paper[3], and it is also proven there that the Euclidean distance is such a metric, which is why our original definition (where the objects are random vectors over specifically ℝ𝑛) works so well. Chances are, I’m not smart enough to prove (or disprove, for that matter) strict negative definiteness for some random-ass metrics. So, in the end, if energy distance proves to be useful in any way, we might have to just throw shit at it and hope that it doesn’t spit out any imaginary numbers. Realistically, we would just use the squared distance anyways (at which point, we can handle negative values), because this is a linkage criterion — we just need to know which pair of clusters minimises the “distance”, regardless of whether that “distance” is squared or not… and regardless of whether it’s a metric or not. Iunno.
In any case, we can now get to the third and most useful formula of them all. By taking the generalisation above, and then replacing the expected value (𝖤[·]) with its concrete (i.e. operating over individual concrete values/samples) analogue, the arithmetic mean, we get:
Between finite sets of concrete values/samples
Let (𝑀, 𝑑) be a metric space. Let 𝐴, 𝐵 ⊆ 𝑀. Let |𝐴| = 𝑛, and |𝐵| = 𝑚. Let 𝐚 ∈ 𝐴, 𝐛 ∈ 𝐵. For the purpose of summation, select all 𝑖, 𝑘 such that 1 ≤ 𝑖, 𝑘 ≤ 𝑛, and all 𝑗, 𝑙 such that 1 ≤ 𝑗, 𝑙 ≤ 𝑚. Then the square of the energy distance between 𝐴 and 𝐵 is defined as follows:
𝐷2(𝐴, 𝐵) ≝ 2 ÷ (𝑛 ⋅ 𝑚) ⋅ ∑∑𝑑(𝐚𝑖, 𝐛𝑗) − 𝑛−2 ⋅ ∑∑𝑑(𝐚𝑖, 𝐚𝑘) − 𝑚−2 ⋅ ∑∑𝑑(𝐛𝑗, 𝐛𝑙).
Wow, that is truly ugly. I guess plain text just isn’t the perfect medium for mathematical typesetting…
Less ugly version
But why tho?
Like UPGMA (and WPGMA, for that matter), this linkage criterion operates based on arithmetic means of individual object distances. Unlike either of those, however, energy distance takes into account intra-cluster distances, in addition to the inter-cluster distances that UPGMA/WPGMA already take into account. Energy distance apparently owes its name to the concept of potential energy in physics — particularly gravitational potential energy in the context of classical mechanics. In this analogy, individual observations are celestial bodies. These bodies are positioned relative to their hypothesised distribution, which acts as the “reference”/“origin”/“zero” point relative to which we measure the bodies’ potential energies. The ideal goal, then, is to minimise the potential energies of these bodies — at this point, the hypothesised distribution best fits the actual data (or, best fits some other abstract distribution, as the case may be).
Footnotes for “Energy distance”
- [↑] A random vector is basically just a fancy name for a vector of zero or more random variables, which all have to be from the same probability space. For example: four flips of a fair coin (each flip having two possible outcomes, both equally likely: {Heads, Tails}) could be represented as a random vector of length four, where each element of the vector is a random variable representing a single coin flip.
- [↑] We actually also need to define a σ-algebra over 𝑀 — call it 𝛴 — such that (𝑀, 𝛴) is a measurable space, so that we can define a probability measure over it. …Actually, it specifically should be a Borel σ-algebra, but who cares…
- [↑] Székely, Gábor J. & Rizzo, Maria L.; “A new test for multivariate normality”; Journal of Multivariate Analysis; vol. 93, iss. 1, pp. 58〜80; 2005-03; ISSN 0047-259X; https://doi.org/10.1016/j.jmva.2003.12.002.
Orderings
I want to take a little break from the heavy-duty statistical/data-mining stuff, and look instead at another kind of mathematical tool in our toolbox. Whereas the statistical stuff is obviously oriented towards the “phenetics-inspired” approach (not that neighbour-joining, clustering, etc. aren’t used in cladistics — they are, but our objects have no genome or anything like that, so…), our “cladistics-inspired” approach requires a different kind of handiwork. Whereas the phenetics-inspired approach requires that we do all of the following (plus probably some more stuff):
- Determine a suitable encoding(s) for the odd jobs.
- Embed the above encoding into some kind of metric space (or, at least something that vaguely looks like it…?).
- Determine a suitable algorithm(s) to taxonomise/cluster/whatever the data.
- Implement the above algorithm(s).
- Interpret the results somehow.
On the other hand, our cladistics-inspired approach is much more hands-on with the classification of the data, because we will not be using statistical methods at all. Instead, we will want to put together our own “““phylogenetic tree””” that expresses the “““ancestral relationships””” between our objects (viz. our odd jobs).
Although I’m pretty sure that I stressed this at least once before, I want to emphasise once again that the inspiration that I’m drawing from biological taxonomy is not supposed to draw a serious analogy; there is little or no actual similarity between the ontology that we have here, and the ontology of life on Earth. That being said, drawing this inspiration proved useful just for two reasons:
- Biological taxonomy is highly developed as a discipline, so it lends many techniques and principles that we can make use of in our own way.
- It gave me some kind of starting point for my thought process.
With that out of the way, let’s take a look at some more tools that we can use to formalise some aspects of our handmade “phylogenetic tree(s)”.
Weak ordering
The first tool comes from order theory, which sounds scary, but never fear. It’s really simple: weak ordering. A weak ordering on a set is just a ranking of the set’s elements, with the stipulation that it’s possible for elements to be tied with one another. Two-way ties, three-way ties, four-way ties, etc. are all possible. For example, if we wanted to rank MapleLegends players by fame, we would expect there to be some ties. Say we have IGN famemesoicanwearmygear[1] (20 fame), IGN VeryNice (69 fame), IGN b14z317 (420 fame), IGN Honsterslut (0 fame), IGN Nice (69 fame), IGN fineStructure (137 fame), IGN BloodshotSclera (420 fame), and IGN sexnumber (69 fame). Then we can impose a weak ordering onto this set of 8 MapleLegends characters, by ordering them by their fame, which we can graphically represent like this:
- b14z317, BloodshotSclera
- fineStructure
- Nice, VeryNice, sexnumber
- famemesoicanwearmygear
- Honsterslut
…Induced by a strict partial order
One of the ways that weak orderings are usually defined is in terms of a partial order — particularly, a strict partial order. The difference between a “strict” ordering and a usual unqualified (not “strict”) ordering is the same as the difference between “<” and “≤”, respectively. “<” is strict because it reads (at least, in the context of real numbers and similar things) “strictly less than”, as opposed to “≤”, which reads as “less than or equal to”. Partial orders are called “partial” because they are not necessarily connected (another word for “connected” is total), which means that even if 𝑎 and 𝑏 are distinct (𝑎 ≠ 𝑏) elements of some poset[2] 𝑆, it is not necessarily true that they are related. In order words, it is not necessarily true that 𝑎 < 𝑏 ∨ 𝑏 < 𝑎. Elements that are unrelated in this way: ¬(𝑎 < 𝑏 ∨ 𝑏 < 𝑎), are said to be incomparable.
The point of mentioning strict partial orders is that, the incomparability itself is a kind of relation. We can think of our above example (with the 8 MapleLegends characters being weakly ordered by fame) in terms of a strict partial order as well: 𝑎 < 𝑏 iff 𝑎 has strictly less fame than 𝑏, and furthermore, 𝑎 and 𝑏 are incomparable iff their fame values are equal. This strict partial order is special, because it has an additional property that not all strict partial orders have. Strict partial orders, by definition, already have:
- Transitivity: 𝑎 < 𝑏 ∧ 𝑏 < 𝑐 → 𝑎 < 𝑐.
- Irreflexivity: ¬(𝑎 < 𝑎).
- Asymmetry: 𝑎 < 𝑏 → ¬(𝑏 < 𝑎).
But now, we have another property that holds, because this strict partial order is not just any strict partial order — it is defined by taking a weak order and making it strict!:
- Transitivity of incomparability: (𝑎 is incomparable to 𝑏) and (𝑏 is incomparable to 𝑐) → 𝑎 is incomparable to 𝑐.
This is easy to see, because the only way that 𝑎 can be incomparable to 𝑏 is if they are tied (equal fame values), and because fame values are just integers, equality between fame values is transitive. So the above definition of “transitivity of incomparability” can be rewritten, using our example, as: (𝑎 has the same fame as 𝑏) and (𝑏 has the same fame as 𝑐) → 𝑎 has the same fame as 𝑐. Which is pretty obvious, right? This is kinda cool, because it means that our weak ordering is actually kinda two orderings at once — if you take one ordering and flip its “strict”ness, you get the other ordering! And they both satisfy nice (but mostly distinct) properties.
Foobeeny
You might reasonably ask exactly how many weak orderings are possible, given a set 𝑆 of |𝑆| = 𝑛 elements. Well, you’re in luck, because these numbers are called the ordered Bell numbers (a.k.a. Fubini numbers): A000670 in the OEIS. The OEIS lists all such numbers for 𝑛 ≤ 20, but looking at the Oddjobs website’s list of odd jobs, 45 odd jobs are listed, there alone. So I wonder, how many unique weak orderings are there for 𝑛 = 45? Well, thankfully we have a handy-dandy recursive formula for calculating the ordered Bell numbers. Let 𝑎(𝑛) be the number of unique weak orderings of a set of 𝑛 elements. For the purpose of summation, sum over all 𝑖 such that 1 ≤ 𝑖 ≤ 𝑛.
𝑎(𝑛) = ∑(𝑛𝖢𝑖 ⋅ 𝑎(𝑛 − 𝑖)).
Wikipedia also offers a direct summation (both finite and infinite; we don’t care about the infinite ones) formula for ordered Bell numbers, which is defined in terms of Stirling numbers of the second kind. Thankfully, Stirling numbers of the second kind can be expressed using a fairly simple combination of factorials, binomial coefficients, and good ol’ fashioned integer exponentiation. So, to calculate the 45th ordered Bell number, I wrote up a little implementation in Python — actually, a few implementations. The mathematical version of the recursive formula is listed above, and for reference, here is the mathematical version of the non-recursive direct summation that I also used (for summation: 0 ≤ 𝑘 ≤ 𝑛, 0 ≤ 𝑗 ≤ 𝑘):
𝑎(𝑛) = ∑∑[(−1)𝑘−𝑗 ⋅ 𝑘𝖢𝑗 ⋅ 𝑗𝑛].
And for each of the two formulæ above, two Python implementations. Thus, a total of four implementations:
fubini.py
def fubini(n):
"""
``fubini(n)`` is the ``n``th Fubini number (a.k.a. the ``n``th ordered Bell
number).
"""
a = 0
for k in range(0, n + 1):
for j in range(0, k + 1):
a += (-1) ** (k - j) * choose(k, j) * j**n
return a
def fubini_gen(n):
"""
``fubini`` defined by ``sum``ming generators, instead of using explicit
loops.
"""
return sum(
sum(((-1) ** (k - j) * choose(k, j) * j**n) for j in range(0, k + 1))
for k in range(0, n + 1)
)
def fubini_rec_naive(n):
"""
Do **not** use this function. It is only here for illustrative purposes,
and is completely useless for any significantly large values of ``n``.
Implements ``fubini`` using a naïve recursive method. I think the runtime
is Ω(n!).
"""
if n == 0:
return 1
return sum(
(choose(n, i) * fubini_rec_naive(n - i)) for i in range(1, n + 1)
)
def fubini_rec(n):
"""
Implements ``fubini`` using recursion, but memoises, in order to make the
performance (read: asymptotic runtime behaviour) reasonable.
<https://en.wikipedia.org/wiki/Dynamic_programming>
"""
memo = {0: 1}
def a(m):
if m in memo:
return memo[m]
fubini_m = sum((choose(m, i) * a(m - i)) for i in range(1, m + 1))
memo[m] = fubini_m
return fubini_m
return a(n)
The first implementation (fubini) is the straightforward, imperative implementation of the second mathematical formula.
The second implementation (fubini_gen) is very similar to the first, but uses generators (combined with the sum built-in function) instead of explicit loops.
The third implementation (fubini_rec_naive) is a naïve implementation of the first mathematical formula (the recursive one). As the fubini_rec_naive implementation itself says: it is very bad. This naïve implementation has a runtime of, as far as I can tell, Ω(𝑛!). This is, to use a highly technical theoretical computer science term, “utterly useless garbage”. The reason that I wrote the naïve implementation, is for illustrative purposes: to show that implementing the recurrence relation as naïvely as possible does actually get you the right answers, but also the heat death of the universe may have already happened by the time that your computation completes.
The fourth implementation (fubini_rec) is a less naïve implementation of the first mathematical formula (the recursive one). This implementation is indeed recursive, but it uses a little dynamic programming trick to avoid a poor asymptotic runtime: memoisation. I did a really shitty, informal performance comparison by running fubini.py with something at the end like: for _ in range(100): f(100). Substitute each one of the four implementations for f, and you get the idea. I ran the script like this five times per implementation, each time with the time command in front, like: time ./fubini.py. For each batch of five, I took the arithmetic mean by summing the times and dividing by five. For the fubini_rec_naive implementation, I took away the loop (no for _ in range(100):, so giving it a 100-fold speed advantage), but as expected, it did not complete. I let it run for 183 seconds, just for laughs I guess… I suspect that it would never actually finish (at least, not in a reasonable, human/deer timescale). I also did the same thing all over again, because I forgot to measure memory usage (/usr/bin/time -v ./fubini.py), and I wanted to see if that was interesting. I actually have a value here for fubini_rec_naive, as I just Ctrl+c’d after 60 seconds of execution time.
| implementation | time (s) | peak memory (KiB) |
|---|---|---|
fubini | 1.130 | 9 144.8 |
fubini_gen | 1.123 | 9 096.0 |
fubini_rec_naive | ≈∞ | 9 180.0 |
fubini_rec | 0.827 | 10 159.2 |
As you can see, all three of the reasonable implementations are pretty comparable performance-wise. fubini_gen looks like it maybe performs slightly better (in space & time) than fubini, but probably not — I’m sure that’s just pure noise. fubini_rec is faster enough that I suspect it really is faster, which is kinda cool! Naïvely, I would expect the straightforward, imperative, direct summation to be the fastest — which would make fubini the fastest (or tied for the fastest). However, it seems that that is not so. However, as expected, fubini_rec does use noticeably more space. Here, the increase looks pretty modest, although I suspect that the actual overhead is larger than it looks here, as most of that memory usage is probably just the Python interpreter/runtime.
Oh, right. We were asking what the 45th ordered Bell number is. Well, it’s this:
1 255 482 482 235 481 041 484 313 695 469 155 949 742 941 807 533 901 307 975 355 741.
That is roughly 1.26 × 1063, or 1.26 vigintillion. For comparison, this is much larger than the estimated number of kilograms of ordinary matter in the observable universe, which is a measly 1.5 × 1053 kg — roughly 10 billion (1010) times smaller than the 45th ordered Bell number. Yikes!!
I literally just forgot what I was doing
I was going to cover some more stuff, but I got distracted. You might ask me: why did we even consider weak orders in the first place? Who cares?? Why am I reading this drivel???
Those are all good questions, although I’m afraid that I can only answer the first one. The reason for considering weak orderings is that when we hand-craft our “phylogenetic tree(s)”, we may want to start with the most skeletal structure possible: ordering our objects (our odd jobs) in roughly “chronological order” (or rather, some notion of “primitiveness”). This will certainly end up being a weak ordering, as there should be many pairs of objects where we just don’t know if one “came first”, the other one “came first”, or they emerged at “the same time”. If 𝑂 is our set of odd jobs, and we had such a pair of objects (𝑎, 𝑏) ∈ 𝑂 × 𝑂, then under our weak ordering (𝑂, ≤), it would be true that 𝑎 ≤ 𝑏 ∧ 𝑏 ≤ 𝑎. We can then impose this ordering, later, onto our tree… or whatever it is. We shall investigate this next time, I guess.
Footnotes for “Orderings”
- [↑] I’m aware that some of these IGNs are too long to be valid. I think (IIRC) that the maximum length is 12 characters long?
- [↑] Partially ordered set.
Grind sesh @ 3–4 F
I was invited by xBowtjuhNL and Gruzz to have a little fun grinding at an unusual location (or, at the very least, unusual for such low-level characters): Sutra Depository 3–4 F. As some readers will know, the Sutra Depository (which is located within the Shaolin Temple part of the Mount Song–Shaolin Temple region of China) is home to several varieties of bald-headed monastic kung fu practitioners. True to their reputation, these humble monks are more than capable of beating the living shit out of you, if you get too close. 3–4 F of the depository, in particular, is home to Bronze Staffmen and, even more concerningly, Silver Spearmen. These Buddhist martial experts have gobs & gobs of HP — a single Silver Spearman, for example, has 4.5 times as much HP as a Jr. Balrog!! But they pay fairly well, if you can best them in combat — that single 225k HP Silver Spearman awards a base EXP of 11 935 (23 870 after a 2× multiplier)!
So we gave it a whirl, with me playing my pure STR bishop cervid:

We weren’t clearing these monks as quickly as I had hoped, so I decided to take charge:
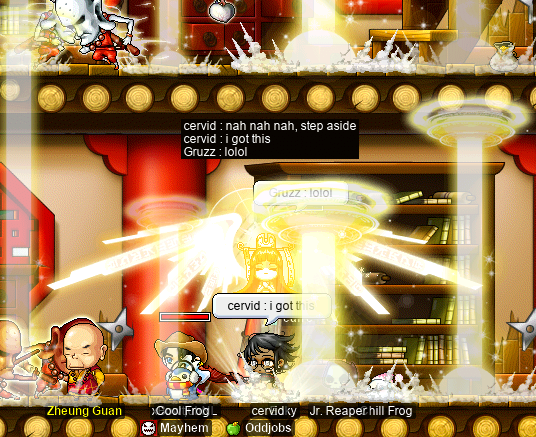
Transcription of the chatlog in the above image
cervid: nah nah nah, step aside
i got this
Gruzz: lolol
That’s right; with Genesis, cervid is capable of a whopping 0(!) aggregate DPM versus these guys. Incroyable.
And, I found that Dooming the monks to turn them into wee blue snails was quite effective:
Basic-attacking Blue Snails is just so much simpler…
A lil bossin’ wif MPQ GANG
I attended some of the usual Papu/Rav, also with Gruzz & xBowtjuhNL, as well as Harlez. Here, I was playing as my darksterity knight rusa. I managed to capture a rather chaotic moment (of which there are plenty, I suppose) during the fight with Papulatus’s 2nd body:
You can’t actually see me in this image, per se… You can see most of the Spear Crusher animation, as well as my pet Rudolph, and even just a few pixels of my weapon (or rather, my NX pet hawk covering up the Sky Ski underneath).
After the Papu fights, we had some fun with Chill Frog trying on various eye accessories. Here is Chill Frog, donning a very stylish snorkel:
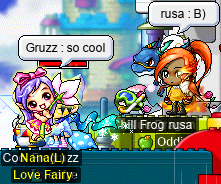
Transcription of the chatlog in the above image
Gruzz: so cool
rusa: B)
And we did Rav runs as well, of course. In which runs, our pets collectively reminded us of just how much they love the Pickpocket skill:
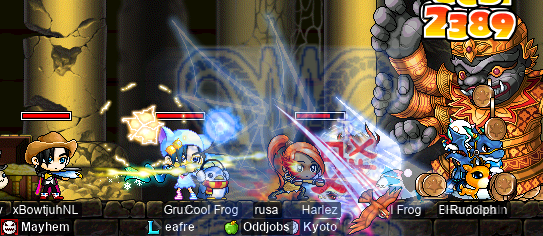
So many shiny cylinders, so little time…
d34r hits level 70!!!
Now that the summer event maintenance was fast approaching, and my Vicloc dagger spearwoman d34r was fast approaching the big level 70, I wanted to make the latter happen first! But first (even more first), of course, the obligatory “even more Jr. Rog hunting” — in futile hopes of a Golden River:

As you can see above, I was joined by Vicloc bandit xXCrookXx (Level1Crook, Lv1Crook) — now in full level 60 swag. Unfortunately, as usual, no luck with Golden River drops. Oh well.
After even more FoG grinding — some of which was solo, some of which was also joined by xXCrookXx — I was joined by crusader Update, who I grinded with for not too long before hitting the fabled level 70:
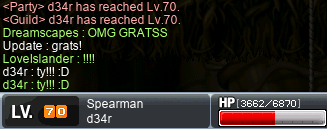
Transcription of the above image
[system message]: ⟨Party⟩ d34r has reached Lv.70.
⟨Guild⟩ d34r has reached Lv.70.
Dreamscapes: OMG GRATSS
Update: grats!
LoveIslander: !!!!
d34r: ty!!! :D
Yayyy!!! First Vicloc level 70! o_o;
I kept grinding with Update for a while afterwards. I also tried my hand at scrolling my only level 70 equip so far — a clean Silver Ancient Shield with very high stats — with my only shield STR scroll so far…
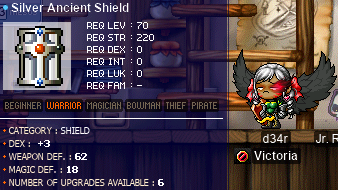
Transcription of the above image
Silver Ancient Shield
- Req lev: 70
- Req STR: 220
- Req class: warrior
- Category: shield
- DEX: +3
- Weapon def.: 62
- Magic def.: 18
- Number of upgrades available: 6
